Fast Matrix Multiplication Approximation on GPUs

Table of Contents

With the rising importance of GPUs as AI accelerators, GPU manufacturers have started to prioritize 16-bit floating point (FP16) over FP32 or FP64 performance. However, many HPC workloads require FP32/FP64 computations for numerical accuracy, but these accelerators often either lack native support for FP64 or execute these operations much slower than lower-precision alternatives, as can be seen in the following table:

GPU	FP16	FP32	FP64
NVIDIA RTX 4080 Super	208.9	52.2	0.8
NVIDIA A100	312	19.5	19.5

Peak floating-point performances of recent GPUs in Tflop/s

Thus, in this project, we examined multiple algorithms allowing to approximate FP32 matrix multiplication with multiple FP16 multiplications. We also investigated FP64 approximation with FP32/FP16, but for the sake of brevity, I won’t cover this here.

Algorithms
#

Markidis’ Scheme
#

The Markidis scheme approximates an FP32 matrix multiplication $C_{32} = A_{32}B_{32}$ with four FP16 matrix multiplications. $A_{32}$ and $B_{32}$ are each split into two FP16 matrices $(A_{16}, \Delta A_{16})$ and $(B_{16}, \Delta B_{16})$ using the following pseudocode with scale = 1:

split2(A32, scale)
{
    A16  = toFP16(A32)
    dA16 = toFP16((A32 - toFP32(A16))*scale)
    return (A16, dA16)
}

Using these splits, the approximation of $C_{32}$ is given by: $$C_{32} = A_{16} B_{16} + \Delta A_{16} B_{16} + A_{16} \Delta B_{16} + \Delta A_{16} \Delta B_{16}$$

Ootomo’s Scheme
#

The Ootomo scheme approximates FP32 matrix multiplication with three FP16 matrix multiplications. It does so by adhering to the Markidis scheme but omits the least contributing product $\Delta A_{16} \Delta B_{16}$. Still, it achieves superior approximation accuracy compared to Markidis by using scale = 2^11 when calling the split2 and accumulating the intermediate Tensor Core results with CUDA Cores during each matrix multiplication. The latter is beneficial as it leads to nearest even rounding instead of toward zero rounding, which is beneficial for precision.

Ozaki’s Scheme
#

The Ozaki scheme is a generalization of the previous two approaches, which supports arbitrary floating-point input and output precisions. Instead of splitting the inputs $A$ and $B$ into two, it splits them into arbitrary numbers $n_A$ and $n_B$ of matrices, which are obtained by successively subtracting fragments from the input matrices, either until they reach zero or until some predetermined number of iterations is exceeded. All $n_A n_B$ products are cast to target precision (FP32 or FP64) before being summed to the final output.

Evaluation Setup
#

We ran experiments on an NVIDIA RTX 4080 Super with 16 GB of VRAM and an NVIDIA A100 with 40 GB of VRAM. To evaluate accuracy, we compute reference results using x86’s 80-bit floating-point registers and report the mean relative error. We evaluate our implementations for the following input ranges, where exp_rand(a, b) generates random floating-point numbers with exponents over a range [a, b]:

Type 1: $A, B \gets $ exp_rand(-15, 14)
Type 2: $A \gets $ exp_rand(-15, 14), $B \gets $ exp_rand(-35, -15)
Type 3: $A, B \gets $ exp_rand(-35, -15)
Type 4: $A \gets $ exp_rand(-100, -35), $B \gets $ exp_rand(-100, 14)

For our approximation scripts we implemented a highly optimized matrix multiplication algorithm on Tensor Cores taking FP16 matrices as input and outputting an FP32 matrix. This article excellently discusses many of the optimizations we applied. All timing and accuracy measurements are performed repeatedly, saved to a JSON file additionally containing metadata and are then automatically visualized through plots. We used a very similar setup in our Image Encryption Optimization project.

Results
#

As expected, the best precision is achieved when accumulating outside the Tensor Cores and scaling, as can be seen in the following figure: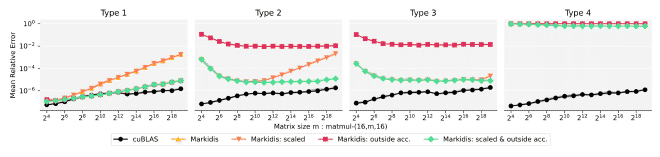

Precision impact of scaling and accumulation outside of Tensor Cores

We also investigated the impact of varying the number of matrix products and splitting matrices into more than two parts (by generalizing the split2 function). This figure shows how more terms always improve precision, with at least three terms needed to almost reach FP32 precision.

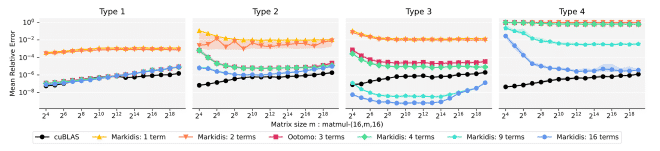
Precision impact of changing the number of multiplicand terms

Thus we can conclude that for matrices with elements not smaller than type 3, using three terms is enough to obtain a good approximation. This allows us to get up to 4x performance improvement compared to native cuBLAS multiplication while offering close to native precision. Here you can see a performance comparison for different square matrix sizes between these two options:

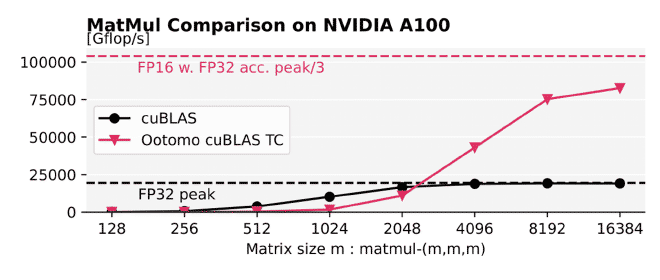
FP32 Performance Ootomo cuBLAS vs. cuBLAS. We used cuBLAS for the A100, as we had limited access to it and thus were unable to optimize our own kernels for it.

As a brief summary, Ootomo’s scheme offers the best trade-off between performance and precision. However, the optimal choice of approximation scheme heavily depends on the exact GPU specifications. For example, we would not be able to get the aforementioned 4x speedup on an RTX 4080 Super using a similar approach due to different peak floating-point configurations.

Our code and benchmarking setup is published on GitHub.

Algorithms#

Markidis’ Scheme#

Ootomo’s Scheme#

Ozaki’s Scheme#

Evaluation Setup#

Results#