Fast image encryption is an essential task in modern communication. While some standard encryption algorithms such as AES are important enough to be supported through fast hardware instructions in most modern CPUs, in this project we developed a fast implementation of the image encryption algorithm described in the paper “A new chaos-based fast image encryption algorithm”.
Algorithm Overview#
As input the encryption algorithm receives a 128-bit key and an RGBA image of size \(w \times h\). The key is used to initialize the spatiotemporal chaos system (NCML), and further defines a pixel permutation of the original image. Next, the image is partitioned into \(w\) blocks of 8x8 pixels. Every block then undergoes an encryption procedure and a new position for the block is computed. If that position is already occupied, the algorithm picks the next available block in ascending order. Finally, a local step updates the NCML state. Notably, this local step introduces considerable sequential dependencies and thus prevents parallel block encryption.
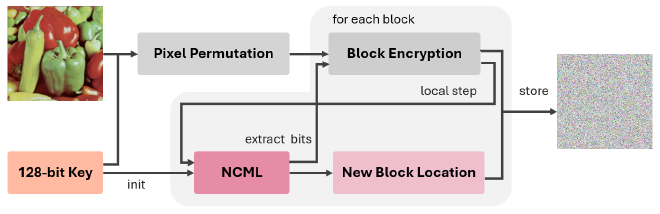
Our Optimizations#
Version 0 - Baseline#
As a baseline, we implemented a straightforward C implementation of the pseudocode given in the original paper.
Version 1 - Flattening#
Version 0 contains multiple nested arrays, with a 2D array for both blocks of the original and cipher image. Every block is explicitly allocated and freed. As the overhead of such memory-related operations can be considerable, we flattened these 3D arrays into linear arrays and only utilized a single malloc/free call. As you can see in the performance comparison figure below, this already yields a substantial speedup for small image sizes. However, the performance for large image sizes is still terrible…
Version 2 - Improved Block Position Search#
Our custom profiler revealed that one step—specifically, searching for an unoccupied block position (Step 4 (iii))—dominated the runtime on large images. For example, when encrypting a 4096×4096 RGBA image, we observed:
--- Profiling encrypt_v1 ---
name total
encrypt_init 0.2 %
encrypt_mainLoop 99.8 %
ncml_generate 0.4 %
Step 4 (ii) 0.3 %
Step 4 (iii) 99.1 %
total time 40.74 sec
More than 99% of the time was spent on this one search step.
To address this, we replaced the original method with a 64-ary search tree.
This structure uses one 64-bit integer per node and requires only 4 levels to accommodate images up to 8192×8192 pixels—resulting in fewer memory jumps than a binary tree.
Additionally, we exploited the x86 intrinsic _mm_tzcnt_64 to quickly find the next zero bit in a node when a position was occupied.
With this redesign, the steps needed to locate a free block scale linearly with the number of tree layers (thus logarithmically with respect to the input size).
Taking a look at our profiler output for the same image size again, we can observe a 95x speedup solely through this optimization. The performance is now also a lot more consistent across image sizes.
--- Profiling encrypt_v2 ---
name total
encrypt_init 14.7 %
encrypt_mainLoop 85.3 %
ncml_generate 40.0 %
Step 4 (ii) 34.3 %
Step 4 (iii) 3.0 %
total time 0.43 sec
Version 3 - Standard C Optimizations#
Up until this version, the algorithm made four strided passes through the input data (one for each color channel). For better spatial locality, we rewrote the algorithm to only perform a single pass through the image data and encrypt all channels at once. Next to some standard C optimizations such as function inlining, loop unrolling and strength reduction, we further incorporated blocking (better cache usage) for the pixel permutation step. We added a simple autotuning infrastructure to determine relevant parameters.
Version 4 - AVX2 Vectorization#
In this version, we accelerated the two major computation hotspots: the NCML random byte generation and the pixel encryption (step 4 (ii)). Since many operations work on individual bytes, we leveraged AVX2’s SIMD capabilities to process multiple bytes in parallel.
For the NCML generation, we broke the process into five stages—lattice update, bit extraction, function application, S-box substitution, and final function application. By handling the initial steps with double-precision floating point operations and then processing the remaining byte-level steps in 128-bit registers (16 bytes per instruction), we avoided the overhead associated with lane-crossing in 256-bit registers.
In particular, we employed the _mm_alignr_epi8 intrinsic to efficiently perform cyclic byte rotations needed for various binary operations.
Another interesting use of a SIMD intrinsic is for the substitution with the AES S-box.
Given the importance of AES, many CPUs offer hardware support for its execution. The _mm_aesenclast_si128 intrinsic performs the last round of the AES encryption flow consisting of a row shift, our desired byte substitution, and an XOR with the round key.
To use this hardware instruction for our purposes, we just use a zero key as the round key, ensuring the XOR operation remains without effect.
Furthermore, we have to revert the performed row shift.
Although these extra steps add a bit of overhead, the performance gain from hardware-accelerated byte substitution more than compensates for it.
Version 5 - AVX512 Vectorization#
As the AMD Ryzen 9 7900 CPU features 512-bit wide registers, we added an AVX-512 version intended as the final and best-performing version. This allowed us to increase parallelism even further and benefit from a much larger set of available instructions.
Results#
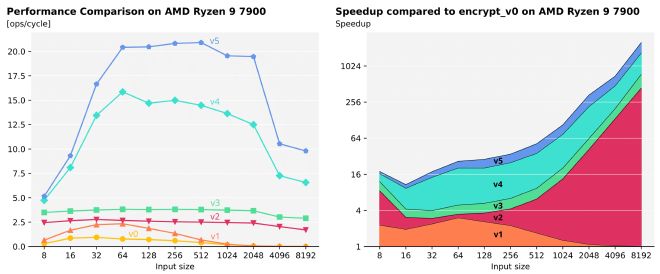
Our overall speedup is smallest (~16x) for the smallest input image size of 8x8 pixels and then grows roughly monotonically up until our maximum overall speedup of ~2500x. As the speedup breakdown shows, the bulk of this improvement comes from our enhanced block position search.
The theoretical peak performance of our CPU for the encryption algorithm, based on the instruction mix, is 4 ops/cycle for scalar performance and 90 ops/cycle for vector performance. This means our best-performing sizes of version 3 achieve 95% of the theoretical scalar peak performance and version 5 achieves 29.5% of the theoretical AVX-512 peak performance. While vectorized performance still has room for improvement, the heavy data dependencies and required shuffles in the algorithm likely contribute to this gap.